- 机器学习本质上是关于泛化的。
- 例如,标准的监督学习场景包括使用有限样本的标记示例来对未见示例做出准确预测。
- 问题通常表述为从假设集中选择一个函数,假设集是所有函数家族的一个子集。
- 选定的函数随后用于标记所有实例,包括未见示例。
- 应该如何选择假设集?
- 假设集丰富或复杂时,学习者可能选择一个与训练样本一致的函数或预测器,即在训练样本上不犯错误的函数。
- 在较不复杂的家族中,训练样本上出现一些错误可能是不可避免的。
- 但是,哪一个将导致更好的泛化?我们应该如何定义假设集的复杂性?
 图
1.2
图
1.2
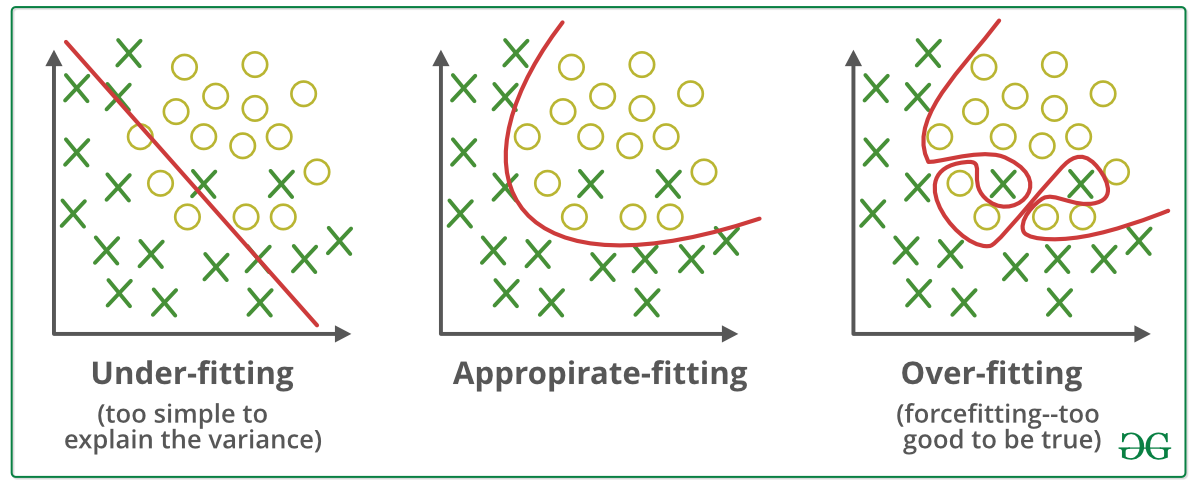
- 左面板上的曲折线在蓝色和红色训练样本上是一致的,
- 但它是一个复杂的分离面,不太可能很好地泛化到未见过的数据。
- 相比之下,右面板上的决策面更简单,尽管它对训练样本中的一些点分类错误,但可能泛化得更好。
- 图1.2说明了这两种类型的解决方案:
- 一种是曲折线,它完美地分离了蓝色和红色点的两个群体,并且是从一个复杂的家族中选择的;
- 另一种是更平滑的线,它来自一个更简单的家族,只能不完全地区分这两个集合。
- 我们将看到,一般来说,训练样本上的最佳预测器可能不是整体上的最佳。
- 从一个非常复杂的家族中选择的预测器本质上可以记住数据,但泛化与训练标签的记忆是不同的。
- 我们将看到样本大小与复杂性之间的权衡在泛化中起着关键作用。
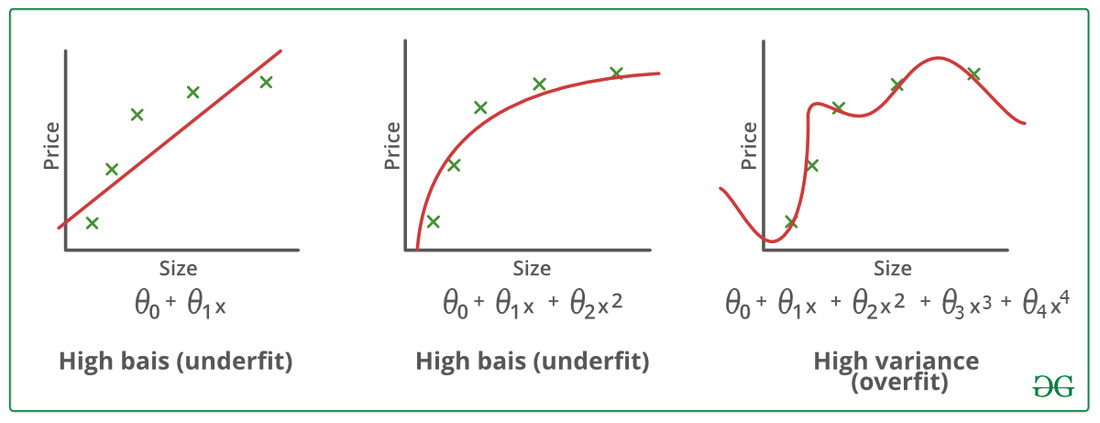
- 当样本大小相对较小时,选择过于复杂的家族可能导致泛化效果差,这也被称为过拟合 (overfitting)。
- 另一方面,如果家族过于简单,可能无法达到足够的准确性,这被称为 欠拟合 (underfitting)。
- 在接下来的章节中,我们将
- 更详细地分析泛化问题,
- 试图为学习推导理论上的保证。
- 这将取决于我们将彻底讨论的不同复杂性概念。
图 1.2

