示例 3.12 超平面

考虑 ${\mathbb{R}}^2$ 中的超平面。

对于 ${\mathbb{R}}^2$ 中的四个点，使用超平面无法实现的二分法。

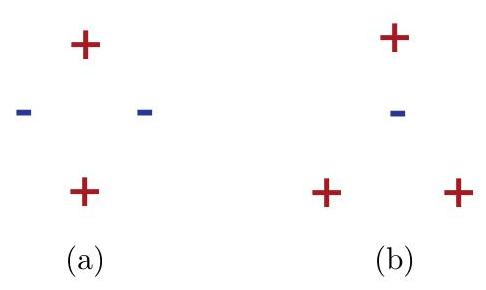
1. 四个点都位于凸包上。
2. 三个点位于凸包上，而剩下的一个点位于内部。

Figure 3.2

我们首先观察到，在 ${\mathbb{R}}^2$ 中，任何 三个 不共线的点都可以被打碎。

• 为了获得前三种二分法，我们选择一个超平面，使得
  • 两个点在一侧，
  • 第三个点在另一侧。
• 为了获得第四种二分法，我们使得
  • 所有三个点都位于超平面的同一侧。
  • 剩下的四种二分法通过简单地切换符号来实现。

接下来，我们通过考虑两种情况来证明 四个 点不能被打碎：

1. 四个点位于由这四个点定义的凸包上，以及
2. 四个点中的三个位于凸包上，剩下的一个点位于内部。 证明
3. 在第一种情况下，无法实现对角线对的正标记和另一对对角线对的负标记，如图 3.2(a) 所示。
4. 在第二种情况下，无法实现对凸包上的点的正标记和对内部点的负标记，如图 3.2(b) 所示。 因此，$\mathrm{VCdim}({\mathbb{R}}^2\text{ 中的超平面})=3$。