python 展示经验分布函数逼近分布函数

我们可以通过 Python 来演示“样本的经验分布函数（Empirical Distribution Function, EDF）如何随着样本量的增加而逼近真实分布函数（True CDF）”。

下面是一个使用 numpy 和 matplotlib 的简单示例，选用标准正态分布作为真实分布：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
 
def plot_edf_vs_cdf(sample_sizes):
    x = np.linspace(-4, 4, 1000)
    true_cdf = norm.cdf(x)  # 标准正态分布的真实 CDF
 
    plt.figure(figsize=(10, 6))
 
    for n in sample_sizes:
        sample = np.random.normal(loc=0, scale=1, size=n)
        sample_sorted = np.sort(sample)
        y = np.arange(1, n+1) / n  # EDF 的阶梯值
        plt.step(sample_sorted, y, label=f'EDF (n={n})', where='post', alpha=0.7)
 
    plt.plot(x, true_cdf, 'k--', label='True CDF (N(0,1))')
    plt.xlabel('x')
    plt.ylabel('CDF')
    plt.title('Empirical Distribution Function vs True CDF')
    plt.legend()
    plt.grid(True)
    plt.show()
 
# 示例：观察样本量为 10, 50, 200 时 EDF 的逼近情况
plot_edf_vs_cdf([10, 50, 200])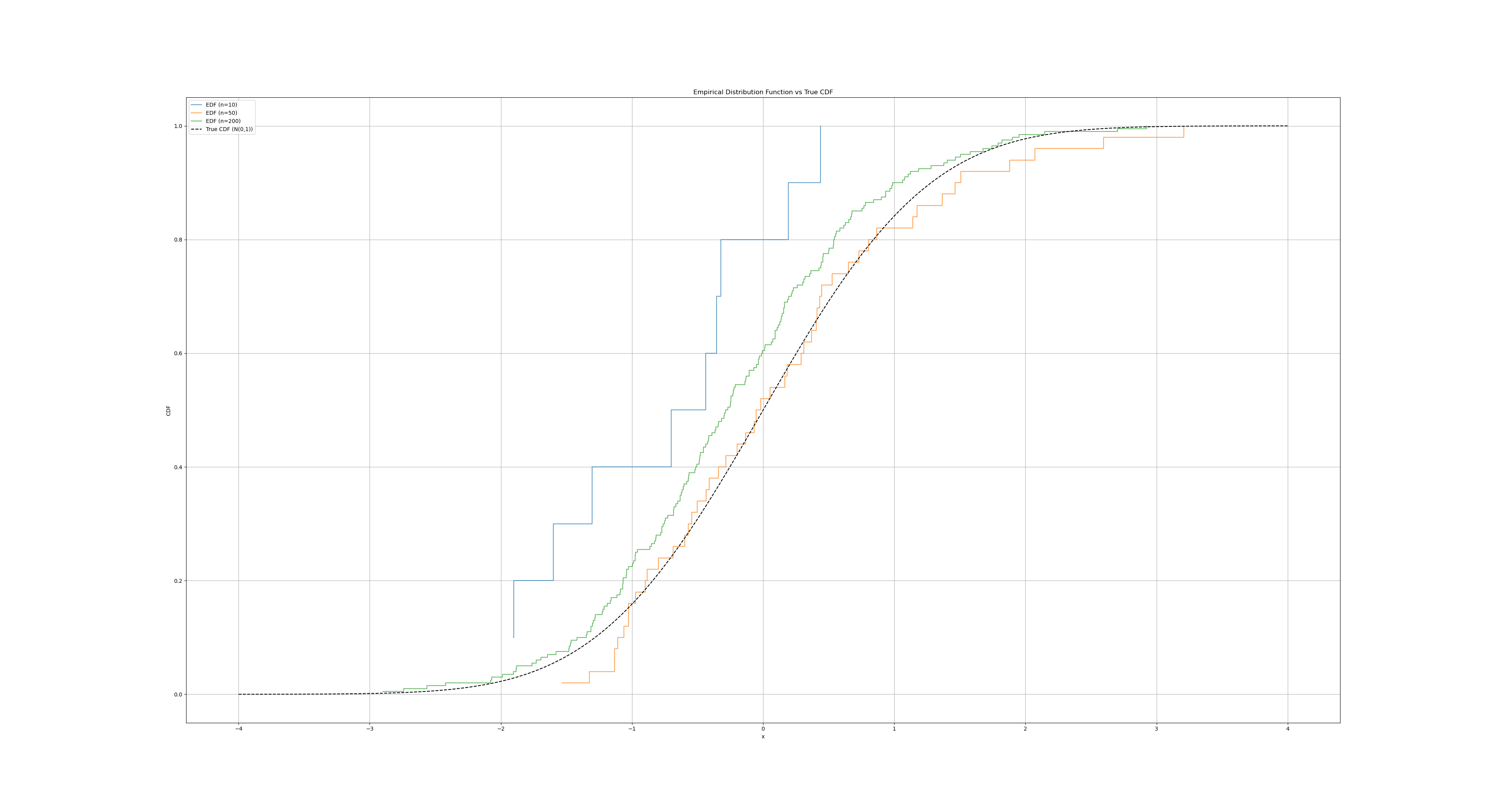

说明：

• step() 用于画经验分布函数的阶梯图；
• norm.cdf(x) 是真实分布函数；
• 可以看到随着样本量的增大，EDF 越来越接近真实的 CDF；
• 如果你多运行几次，每次的EDF都会有波动，但总体趋势是一致的。