python 绘制正态分布

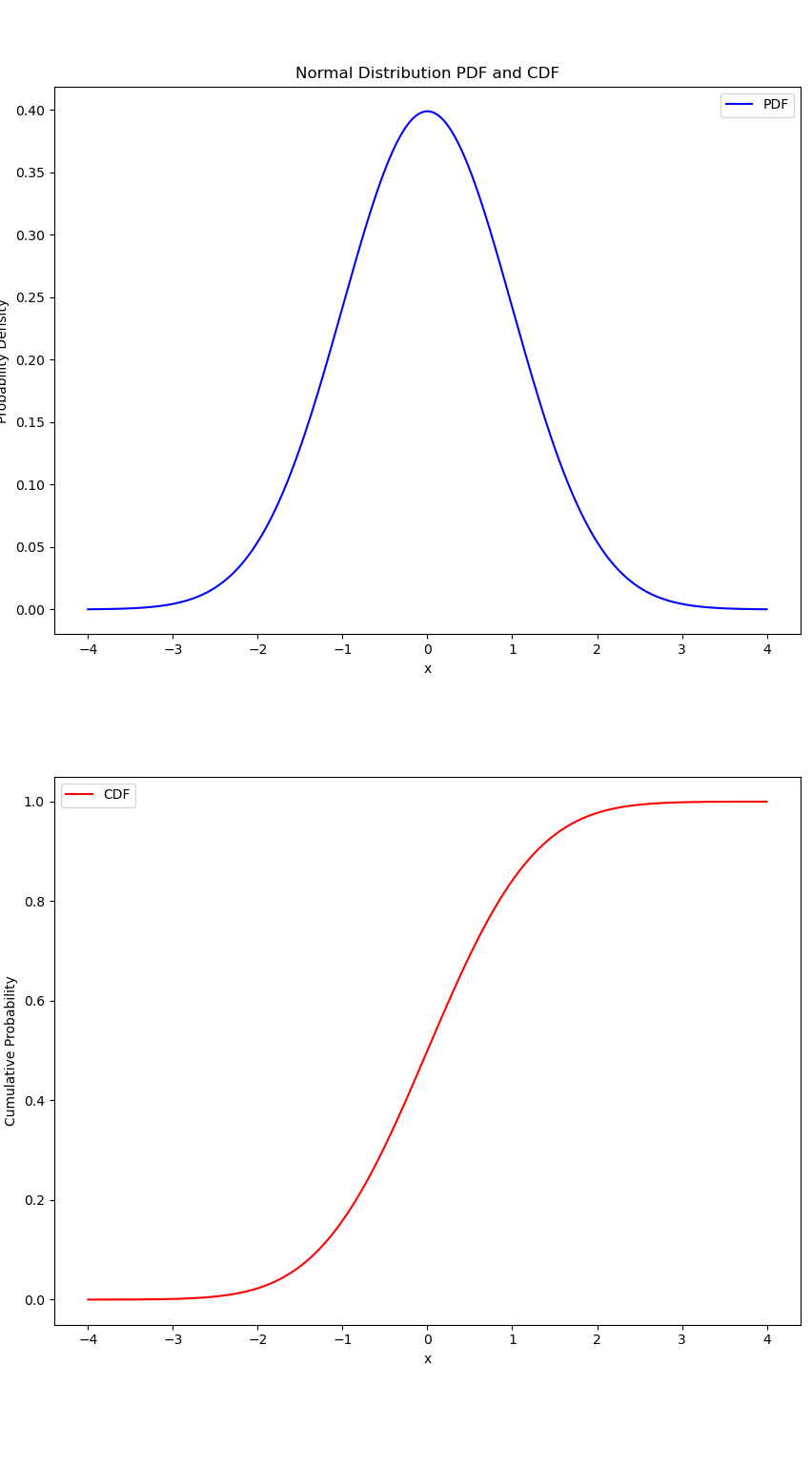
pdf and cdf

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
 
# 定义正态分布的参数
mu = 0    # 均值
sigma = 1 # 标准差
 
# 定义 x 的取值范围
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
 
# 计算 PDF（概率密度函数）
pdf = norm.pdf(x, mu, sigma)
 
# 计算 CDF（累积分布函数）
cdf = norm.cdf(x, mu, sigma)
 
# 作图
plt.figure(figsize=(10, 6))
 
# 画 PDF（近似 PMF）
plt.subplot(2, 1, 1)
plt.plot(x, pdf, label='PDF', color='blue')
plt.title('Normal Distribution PDF and CDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
 
# 画 CDF
plt.subplot(2, 1, 2)
plt.plot(x, cdf, label='CDF', color='red')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.legend()
 
# 调整布局并显示
plt.tight_layout()
plt.show()

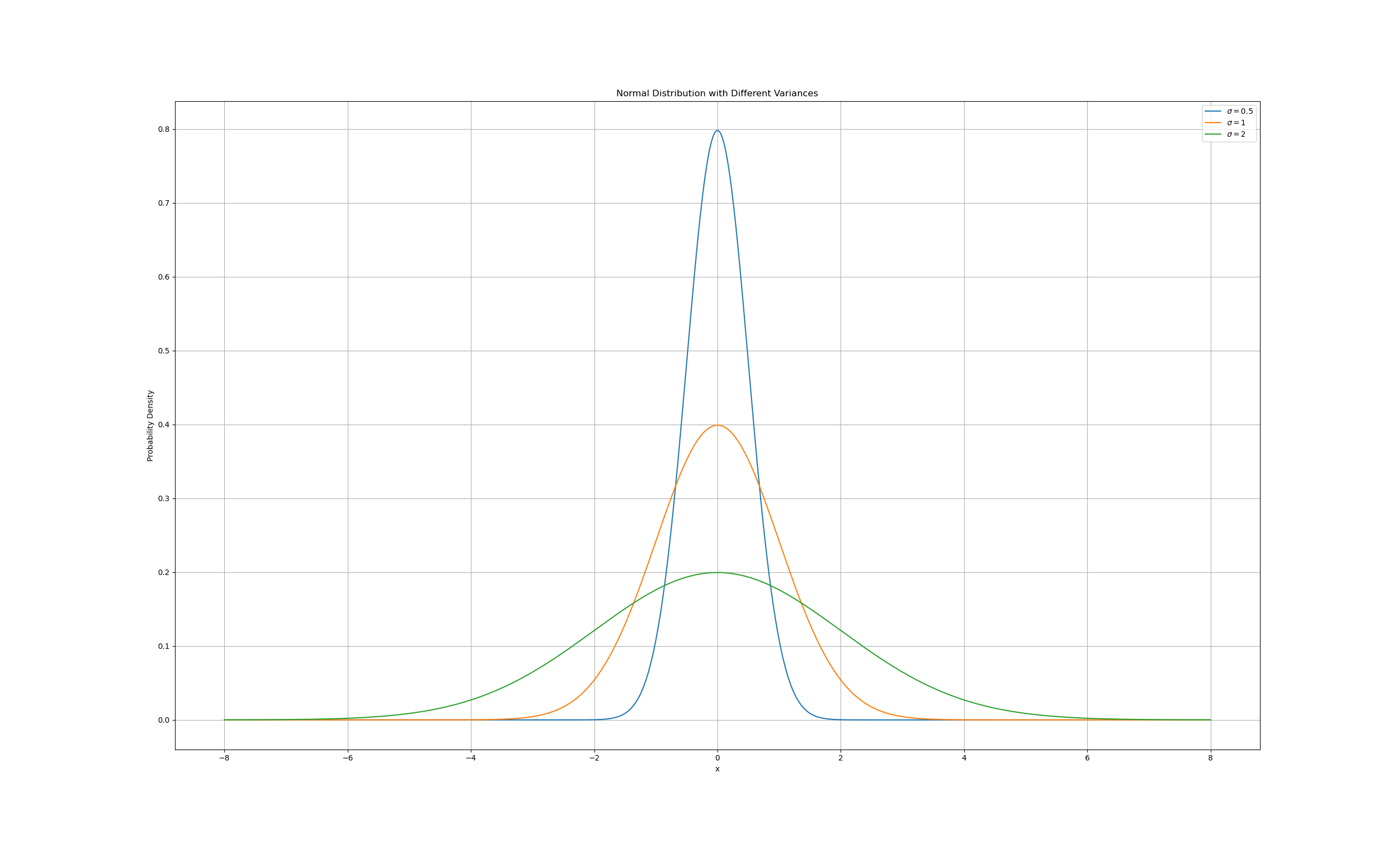
different sigma

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
 
# 定义均值
mu = 0
 
# 定义不同的标准差
sigmas = [0.5, 1, 2]
 
# 定义 x 的取值范围（根据最大标准差调整范围）
x = np.linspace(mu - 4*max(sigmas), mu + 4*max(sigmas), 1000)
 
# 作图
plt.figure(figsize=(10, 6))
 
# 遍历不同的标准差，绘制对应的正态分布
for sigma in sigmas:
    pdf = norm.pdf(x, mu, sigma)
    plt.plot(x, pdf, label=f'$\sigma={sigma}$')
 
# 添加标题和标签
plt.title('Normal Distribution with Different Variances')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
 
# 显示图像
plt.grid()
plt.show()