4.1.3 随机变量的矩

刻画随机变量的分布特性的另一类数字特征就是随机变量的矩. 我们这里做简单介绍.

定义 4.1.4 (矩)

设 $X$ 为随机变量, $c$ 为常数, $k$ 为正整数, 如果 $E\left[{\left|X-c\right|}^k\right]<\infty$,

$$E\left[{\left(X-c\right)}^k\right]\text{\hspace{1em}(4.1.10)}$$

为 $X$ 关于点 $c$ 的 $k$ 阶矩.

• 当 $c=0$ 时,称 $E\left[X^k\right]$ 为 $X$ 的 $k$ 阶原点矩.
• 当 $c=E\left[X\right]$ 时,称 $E\left[{\left(X-E\left[X\right]\right)}^k\right]$ 为 $X$ 的 $k$ 阶中心矩.

Link to original

由定义 (4.1.4) 看出,

• $X$ 的均值就是 $X$ 的 1 阶原点矩,
• $X$ 的方差就是 $X$ 的 2 阶中心矩.

由 2 阶、3 阶和 4 阶中心矩可以定义两种刻画随机变量分布特性的常用的数字特征, 它们是偏度和峰度.

定义 4.1.5 (偏度 峰度)

设 $X$ 为随机变量, 如果 $E\left[X^4\right]<\infty$,则

• 称 \frac{E\left\lbrack {\left( X - E\left\lbrack X\right\rbrack \right) }^{3}\right\rbrack }{{\left( \operatorname{Var}\left\lbrack X\right\rbrack \right) }^{3/2}} \tag{4.1.11}为 $X$ 的偏度.
• 称 \frac{E\left\lbrack {\left( X - E\left\lbrack X\right\rbrack \right) }^{4}\right\rbrack }{{\left( \operatorname{Var}\left\lbrack X\right\rbrack \right) }^{2}} \tag{4.1.12}为 $X$ 的峰度.

Link to original

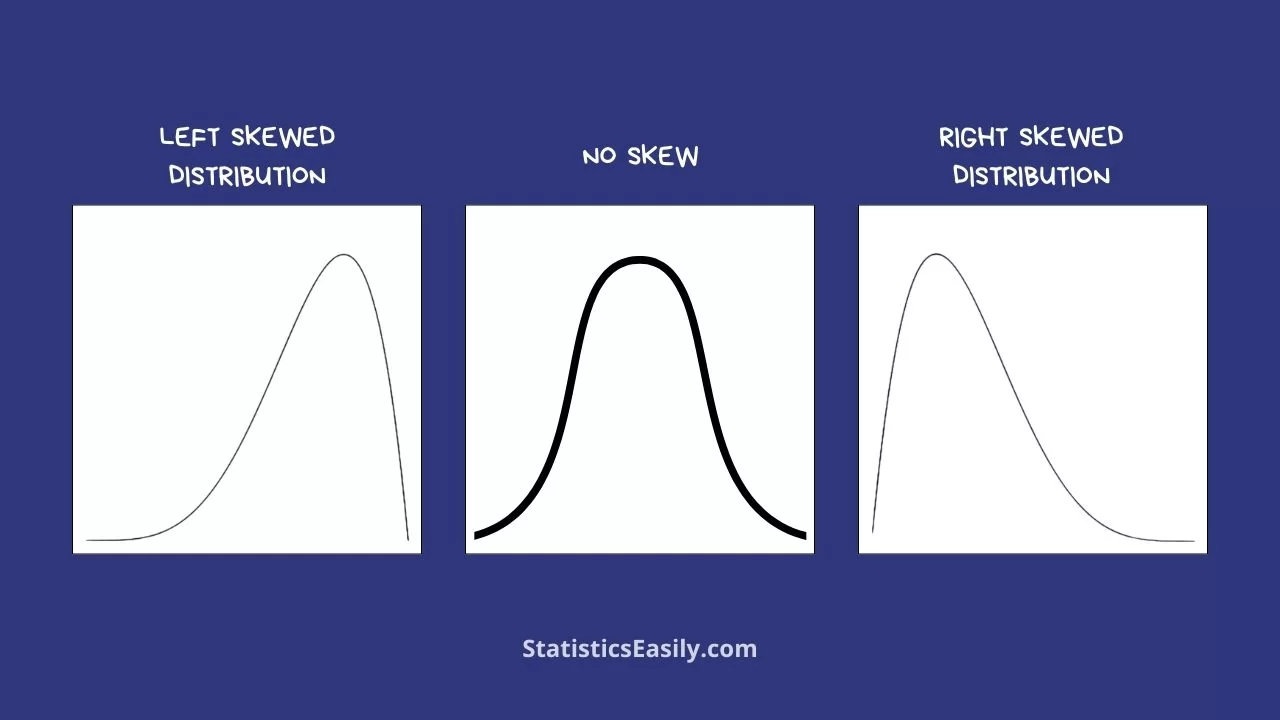
顾名思义,偏度是刻画 $X$ 的分布的偏斜程度.

• 如果 $X$ 的分布关于 $E\left[X\right]$ 对称. 显然 3 阶矩 $E\left[{\left(X-E\left[X\right]\right)}^3\right]=0$, 从而偏度为 0.
• 如果 $E\left[{\left(X-E\left[X\right]\right)}^3\right]>$ 0, 则 $X$ 的分布取值大于 $E\left[X\right]$ 的概率较大,此时称 $X$ 的分布为右偏.
• 如果 $E\left[{\left(X-E\left[X\right]\right)}^3\right]<0$,则称 $X$ 的分布为左偏. (4.1.11) 中除以 ${\left(\mathrm{Var}\left[X\right]\right)}^{3/2}$ 则是为了标准化, 以消除因尺度选择不同所造成的影响. 显然, 正态分布的偏度为 0.

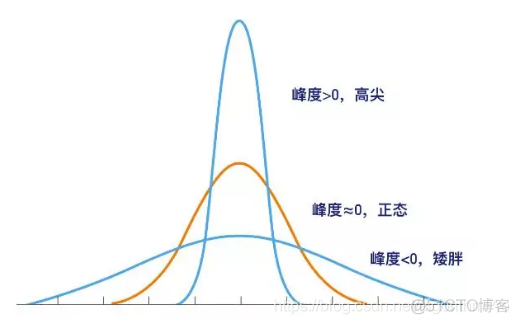
峰度则反映 $X$ 的分布 (密度) 在其均值附近的陡峭程度. 若 $X$ 的取值比较集中于 $E\left[X\right]$ 附近,则峰度较小,否则就比较大. 在 (4.1.12) 中分母出现 ${\left(\mathrm{Var}\left[X\right]\right)}^2$ 也是为了消除尺度的影响而标准化的.

若 $X\sim N\left(\mu ,{\sigma }^2\right)$, 经计算可知 $E\left[{\left(X-\mu \right)}^4\right]=3{\sigma }^4$, 此时 $X$ 的峰度系数为 3. 通常若一个随机变量的峰度系数大于 3, 则称为尖峰的.

• 3.17